Linear Algebra

此处用于记录我学习 MIT 18.06 Linear Algebra 的笔记。

顺便学习 Latex 排版。

每次看完都会忘记，比较难受，尝试记住

线性无关

当一组向量 $v_1, v_2, \ldots, v_n$ 满足以下条件时，称其为线性无关：

$c_1 v_1 + c_2 v_2 + \ldots + c_n v_n = 0 \Rightarrow c_1 = c_2 = \ldots = c_n = 0$

否则称其为线性相关。

向量组 $A$ 线性无关的充要条件是 $R(A) = n$，其中 $n$ 是向量的个数。

可以通过行简化阶梯形矩阵来判断向量组是否线性无关，如果矩阵 $A$ 的行简化阶梯形矩阵有 $n$ 个主元，则向量组线性无关，否则线性相关。

向量组 $A$ 和 $B$ 等价的充要条件是 $R(A) = R(B) = R([A, B])$。

$\beta$ 能被向量组 $A$ 线性表示的充要条件是 $R(A) = R([A, \beta])$。

Tip: 非主元列 $\alpha$ 为 $\begin{pmatrix} c_1, c_2, \ldots, c_n \end{pmatrix}$，则 $\alpha$ 的线性表示为 $\alpha = - \sum_{i} \frac{c_i}{c_j} e_i$，其中 $e_i$ 是主元列。(即取主元，然后组合 $\alpha$ 的每一个元素)

• 若 $R(A) \le R(B)$，不能推出 $A$ 可以被 $B$ 线性表示。

• 若 $\alpha_1, \alpha_2, \ldots, \alpha_n$ 线性相关，不能推出 $\alpha_i$ 可以被其他向量线性表示。

线性方程组的解

设有线性方程组 $Ax = b$，其中 $A$ 是 $m \times n$ 矩阵，$x$ 是 $n \times 1$ 向量，$b$ 是 $m \times 1$ 向量。

考虑 $Ax=b$：

• 有解 -> $R(A) = R([A, b])$
• • 唯一解 -> $R(A) = n$
• • 无穷多解 -> $R(A) < n$
• 无解 -> $R(A) < R([A, b])$

考虑齐次线性方程组 $Ax = 0$：

• R(A) = n -> 唯一解 $x = 0$
• R(A) < n -> 无穷多解

---

从几何上看，线性方程组 $Ax = b$ 有解，表示向量 $b$ 可以被矩阵 $A$ 的列空间线性表示。

如果有唯一解，表示矩阵 $A$ 的列空间是 $\mathbb{R}^m$，且矩阵 $A$ 的列向量线性无关。

如果有无穷多解，表示矩阵 $A$ 的列空间是 $\mathbb{R}^m$，但矩阵 $A$ 的列向量线性相关。

如果无解，表示向量 $b$ 不在矩阵 $A$ 的列空间内。

正交矩阵 Orthogonal Matrix

正交矩阵有 $Q$ 满足 $Q^T Q = I$。

因为 $Q$ 的每一列 $q_i$ 都是单位向量，并且两两正交，所以 $q^T q = 1$。

因此，在 $Q$ 和 $Q^T$ 相乘时，对应元素为 $Q_i * Q_j^T$。只有当 $i = j$ 时，才会有非零值，且为 1。否则任意两列 $q_i$ 和 $q_j$ 的互相垂直，内积为 0。

此外，因为有 $Q^T Q = I$，所以 $Q^{-1} = Q^T$。

正交矩阵的几何意义

矩阵 $Q$ 进行变换时，$Q$ 会保持向量的长度和角度不变，然后变换基，也可以理解为旋转和镜像。

Schmidt Orthogonalization 施密特正交化

给定一组线性无关的向量 $a_1, a_2, \ldots, a_n$，可以通过施密特正交化将其转换为一组正交向量 $q_1, q_2, \ldots, q_n$。

具体步骤如下：

1. 设 $q_1 = a_1$。

2. 对于 $k = 2, 3, \ldots, n$，计算 $a_k$ 在 $q_1, q_2, \ldots, q_{k-1}$ 上的投影，并将其从 $a_k$ 中减去：

   $$proj_{q_i}(a_k) = \frac{a_k^T q_i}{q_i^T q_i} q_i$$

   $$u_k = a_k - \sum_{i=1}^{k-1} proj_{q_i}(a_k)$$

3. 将 $u_k$ 归一化，得到 $q_k$：

   $$q_k = \frac{u_k}{||u_k||}$$

通过上述步骤，可以得到一组正交向量 $q_1, q_2, \ldots, q_n$。

举例来说，给定向量 $a_1 = \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}$ , $a_2 = \begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix}$ 和 $a_3 = \begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix}$。

1. 设 $q_1 = a_1 = \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}$。

2. 计算 $a_2$ 在 $q_1$ 上的投影：

   $$proj_{q_1}(a_2) = \frac{a_2^T q_1}{q_1^T q_1} q_1 = \frac{\begin{bmatrix} 1 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}}{\begin{bmatrix} 1 & 1 & 0 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}} \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} = \frac{1}{2} \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 0.5 \\ 0.5 \\ 0 \end{bmatrix}$$

   然后计算 $u_2$：

   $$u_2 = a_2 - proj_{q_1}(a_2) = \begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix} - \begin{bmatrix} 0.5 \\ 0.5 \\ 0 \end{bmatrix} = \begin{bmatrix} 0.5 \\ -0.5 \\ 1 \end{bmatrix}$$

3. 然后计算 $u_3$:

   计算 $a_3$ 在 $q_1$ 和 $q_2$ 上的投影：

   $$proj_{q_1}(a_3) = \frac{a_3^T q_1}{q_1^T q_1} q_1 = \frac{\begin{bmatrix} 0 & 1 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}}{\begin{bmatrix} 1 & 1 & 0 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}} \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} = \frac{1}{2} \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 0.5 \\ 0.5 \\ 0 \end{bmatrix}$$

   $$proj_{q_2}(a_3) = \frac{a_3^T q_2}{q_2^T q_2} q_2 = \frac{\begin{bmatrix} 0 & 1 & 1 \end{bmatrix} \begin{bmatrix} 0.5 \\ -0.5 \\ 1 \end{bmatrix}}{\begin{bmatrix} 0.5 & -0.5 & 1 \end{bmatrix} \begin{bmatrix} 0.5 \\ -0.5 \\ 1 \end{bmatrix}} \begin{bmatrix} 0.5 \\ -0.5 \\ 1 \end{bmatrix} = \frac{0.5}{1.5} \begin{bmatrix} 0.5 \\ -0.5 \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{1}{6} \\ -\frac{1}{6} \\ \frac{1}{3} \end{bmatrix}$$

   然后计算 $u_3$：

   $$u_3 = a_3 - proj_{q_1}(a_3) - proj_{q_2}(a_3) = \begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix} - \begin{bmatrix} 0.5 \\ 0.5 \\ 0 \end{bmatrix} - \begin{bmatrix} \frac{1}{6} \\ -\frac{1}{6} \\ \frac{1}{3} \end{bmatrix} = \begin{bmatrix} -\frac{2}{3} \\ \frac{2}{3} \\ \frac{2}{3} \end{bmatrix}$$

4. 最后归一化得到

   $$q_1 = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}, q_2 = \frac{1}{\sqrt{6}} \begin{bmatrix} 1 \\ -1 \\ 2 \end{bmatrix}, q_3 = \frac{1}{\sqrt{3}} \begin{bmatrix} -1 \\ 1 \\ 1 \end{bmatrix}$$

行列式 Determinant

行列式是一个标量值，表示矩阵的某些性质。对于 $n \times n$ 矩阵 $A$，其行列式记为 $det(A)$ 或 $|A|$。

行列式有三个重要性质：

1. The determinant of the n by n identity matrix is 1. 即 $det(I) = 1$。

2. The determinant changes sign when two rows are exchanged. 即交换矩阵的两行，行列式的值会变号。

3. The determinant is a linear function of each row separately. 即行列式对每一行都是线性函数。

   • 如果矩阵的一行乘以一个标量 $k$，则行列式也乘以 $k$。

   • 如果矩阵的一行是两行之和，则行列式等于这两行分别拆分计算的行列式之和。

利用这三个性质，可以推导出其他性质：

4. 如果矩阵有两行相同，则行列式为 0。

   因为根据性质 2，交换这两行会使行列式变号，但行列式并没有发生变化，所以行列式必须为 0。

5. 将行列式的一行加上或者减去另一行，行列式的值不变。

   因为根据性质 3，行列式是线性函数，所以可以将该行拆分成两部分，一部分是原来的行，另一部分是被加上或者减去的行。

   同时，拆分出来的矩阵，将所乘的标量提出后，会有两行相同，根据性质 4，行列式为 0。因此，行列式相加后的值不变。

6. 如果行列式有全零行，那么行列式为 0。

   因为可以将该行加上或者减去其他行，变成两行相同的情况，根据性质 5，行列式的值不变，又因为根据性质 4，所以行列式为 0。

7. 如果行列式是三角矩阵（上三角矩阵或者下三角矩阵），则行列式等于对角线元素的乘积。

   因为可以通过将非对角线元素所在的行加上或者减去其他行，将其变成对角矩阵，而根据性质 3，提出每一行的对角线上的标量后，留下的矩阵是单位矩阵，行列式为 1。

   因此，行列式等于对角线元素的乘积。

8. 如果 $A$ 是奇异矩阵，则 $det(A) = 0$。如果 $A$ 是可逆的矩阵，则 $det(A) \neq 0$。

   将矩阵化为行阶梯形矩阵时，奇异矩阵会有全零行，根据性质 6，行列式为 0。

9. $det(AB) = det(A) \cdot det(B)$。

10. $det(A^{-1}) = \frac{1}{det(A)}$。

    当 $B = A^{-1}$ 时，有 $det(AB) = det(I) = 1$，根据性质 9，$det(AB) = det(A) \cdot det(B)$，所以 $det(A) \cdot det(A^{-1}) = 1$，即 $det(A^{-1}) = \frac{1}{det(A)}$。

11. $det(A^T) = det(A)$。

    当 $A$ 不是奇异矩阵时，有 $A A^{-1} = I$，可以分解为 $PA = LU$，其中 $P$ 是置换矩阵，$L$ 是下三角矩阵，$U$ 是上三角矩阵。

    因为 $det(P) = det(P^T)$，因为 $P^TP = I$

    $det(L) = det(L^T)$，因为 $L$ 的对角线上都 1

    $det(U) = det(U^T)$，因为上下三角矩阵的行列式只取决于对角线元素

    所以 $det(A) = det(P) det(L) det(U) = det(P^T) det(L^T) det(U^T) = det(A^T)$。

    当 $A$ 是奇异矩阵时，$det(A) = 0$，同样有 $det(A^T) = 0$。

因为性质 11，因此行列式的行和列操作是一样的。

行列式的几何意义

行列式的绝对值表示矩阵变换后，空间的变化倍数，或者以单位立方体为例的体积变化倍数。

如果 $det(A) > 0$，表示变换保持了空间的定向；如果 $det(A) < 0$，表示变换改变了空间的定向（例如镜像反转）。

特例有 $det(I) = 1$，表示单位立方体的体积没有变化，空间没有变化。

范德蒙德行列式

设有 $n$ 个不同的数 $x_1, x_2, \ldots, x_n$，则范德蒙德行列式定义为：

$$V = \begin{vmatrix} 1 & x_1 & x_1^2 & \ldots & x_1^{n-1} \\ 1 & x_2 & x_2^2 & \ldots & x_2^{n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_n & x_n^2 & \ldots & x_n^{n-1} \end{vmatrix}$$

范德蒙德行列式的值为：

$$V = \prod_{1 \leq i < j \leq n} (x_j - x_i)$$

迹 Trace

迹是矩阵对角线元素的和，记为 $tr(A)$。

迹同时也是特征值之和，因此迹的几何意义可以看作矩阵对空间的平均拉伸，尽管没有平均掉（没有除以 $dim(A)$）。

特征向量与特征值 Eigenvectors and Eigenvalues

设有矩阵 $A$，如果存在向量 $x$ 和标量 $\lambda$，使得 $A x = \lambda x$，则称 $x$ 为矩阵 $A$ 的特征向量，$\lambda$ 为对应的特征值。

因此有

$$A x - \lambda x = 0 \Rightarrow (A - \lambda I)x = 0$$

要使得 $(A - \lambda I)x = 0$ 有非零解，必须使得 $A - \lambda I$ 为奇异矩阵，$det(A - \lambda I) = 0$。

求特征值 Finding Eigenvalues

要找到矩阵 $A$ 的特征值，需要解特征多项式 $det(A - \lambda I) = 0$。 该多项式的根即为矩阵 $A$ 的特征值。可能是重根。

求特征向量 Finding Eigenvectors

对于每个特征值 $\lambda$，将其代入方程 $(A - \lambda I)x = 0$，通过求解该齐次线性方程组，可以找到对应的特征向量 $x$。特征向量不一定唯一，当特征值是重根时，可能有多个线性无关的特征向量。

---

$A^{-1} x = \lambda^{-1} x$，因此，$A$ 的特征值的倒数是 $A^{-1}$ 的特征值，特征向量相同。

证明如下：

$$A x = \lambda x$$

$$(A^{-1} A) x = A^{-1} \lambda x$$

$$Ix = \lambda (A^{-1} x)$$

$$A^{-1} x = \lambda^{-1} x$$

---

矩阵的幂次的特征值是对应特征值的幂次：

$$(A^k) x = \lambda^k x$$

---

此外，矩阵的行列式等于其特征值的乘积：

$$det(A) = \lambda_1 \cdot \lambda_2 \cdot \ldots \cdot \lambda_n$$

---

矩阵的迹等于其特征值的和：

$$tr(A) = \lambda_1 + \lambda_2 + \ldots + \lambda_n$$

---

两个矩阵相加的特征值等于各自特征值的和并不总是成立，因为特征向量大多数情况下不同，但是同一矩阵内，矩阵多项式的特征值等于矩阵的特征值的多项式值。见 矩阵的多项式、对角化与特征值 部分。

特征值和特征向量的几何意义

从几何上看，实特征值对应的是矩阵对特征向量（输入向量）方向进行伸缩变换，而复特征值对应的是矩阵对输入向量进行旋转变换。

不同特征值的特征向量线性无关：

假设有 $A x_1 = \lambda_1 x_1$ 和 $A x_2 = \lambda_2 x_2$，其中 $\lambda_1 \neq \lambda_2$。

假设 $k x_1 = x_2$，代入方程：

$$A (k x_1) = \lambda_2 (k x_1)$$

$$k (A x_1) = k (\lambda_2 x_1)$$

$$A x_1 = \lambda_2 x_1$$

与 $\lambda_1 \neq \lambda_2$ 矛盾，因此 $x_1$ 和 $x_2$ 线性无关。

对角化 Diagonalization

如果一个矩阵 $A$ 有 $n$ 个线性无关的特征向量 $x_1, x_2, \ldots, x_n$，则可以将这些特征向量组成一个矩阵 $X = [x_1, x_2, \ldots, x_n]$。对应的特征值组成对角矩阵 $\Lambda = diag(\lambda_1, \lambda_2, \ldots, \lambda_n)$。

则有 $A X = X \Lambda$。如果 $X$ 可逆，则可以写成 $A = X \Lambda X^{-1}$，称为矩阵 $A$ 的对角化形式。

因为 $X$ 需要可逆，因此需要 A 有 $n$ 个线性无关的特征向量。必须满足矩阵 $A$ 的特征多项式有 $n$ 个不同的根，或者重根的代数重数等于几何重数。

有了对角化形式后，可以方便地计算矩阵的幂次 $A^k = X \Lambda^k X^{-1}$，其中 $\Lambda^k$ 只需对角线元素取幂。

矩阵的多项式、对角化与特征值

对于求矩阵多项式 $p(A) = a_0 I + a_1 A + a_2 A^2 + \ldots + a_k A^k$，如果知道矩阵 $A$ 可以对角化，可以简化计算。

设 $A = X \Lambda X^{-1}$， 则有

$$p(A) = a_0 I + a_1 (X \Lambda X^{-1}) + a_2 (X \Lambda X^{-1})^2 + \ldots + a_k (X \Lambda X^{-1})^k$$

$$= a_0 I + a_1 X \Lambda X^{-1} + a_2 X \Lambda^2 X^{-1} + \ldots + a_k X \Lambda^k X^{-1}$$

$$= X (a_0 I + a_1 \Lambda + a_2 \Lambda^2 + \ldots + a_k \Lambda^k) X^{-1}$$

$$= X p(\Lambda) X^{-1}$$

其中 $p(\Lambda)$ 只需对角线元素取多项式值即可。

这将对 $A$ 的多项式计算简化为对对角矩阵 $\Lambda$ 的多项式，或者是对角元素的多项式计算。

---

此外，对于 $\det(p(A))$ 如果已知矩阵 $A$ 的特征值 $\lambda_1, \lambda_2, \ldots, \lambda_n$

$$\det(p(A)) = p(\lambda_1) \cdot p(\lambda_2) \cdot \ldots \cdot p(\lambda_n)$$

对称矩阵 Symmetric Matrix

当矩阵 $S$ 满足 $S = S^T$ 时，称其为对称矩阵。

回顾上面的对角化，可以得到 $S = X \Lambda X^{-1}$。

由于 $S$ 是对称矩阵，有 $S = S^T$，因此 $X \Lambda X^{-1} = (X \Lambda X^{-1})^T = (X^{-1})^T \Lambda^T X^T$。

$\Lambda$ 是对角矩阵，因此 $\Lambda^T = \Lambda$。

因此有 $X \Lambda X^{-1} = (X^{-1})^T \Lambda X^T$。

两边同时左乘 $X^{-1}$，右乘 $X$，得到 $\Lambda = X^{-1} (X^{-1})^T \Lambda X^T X$。

所以 $X$ 满足 $X^{-1} = X^T$，即 $X$ 是正交矩阵。

因此，对称矩阵可以被正交对角化，即 $S = Q \Lambda Q^T$，其中 $Q$ 是正交矩阵，$\Lambda$ 是对角矩阵。

对称矩阵的以下性质：

1. 特征值为实数。

2. 不同特征值对应的特征向量正交。

---

假设实矩阵 $S$ 有 $Sx = \lambda x$, $\lambda = a + bi$, 则一定有 $S \bar{x} = \bar{\lambda} \bar{x}$。

对于 $Sx = \lambda x$，两边左乘 $\bar{x}^T$，得到 $\bar{x}^T S x = \lambda \bar{x}^T x$。

对于 $S \bar{x} = \bar{\lambda} \bar{x}$，两边右乘 $x$，得到 $\bar{x}^T S x = \bar{\lambda} \bar{x}^T x$。

对比可知 $\lambda \bar{x}^T x = \bar{\lambda} \bar{x}^T x$，当且仅当 $\bar{x}^T x \neq 0$ 时，$\lambda = \bar{\lambda}$，即 $\lambda$ 为实数。

如何证明 $\bar{x}^T x \neq 0$ 呢？

假设 $\bar{x} = a + bi$，则 $\bar{x}^T x = (a - bi)^T (a + bi) = a^T a + b^T b$，因为 $a$ 和 $b$ 不全为 0，所以 $a^T a + b^T b > 0$。

因此，实对称矩阵的特征值为实数。

Real Eigenvalues All the eigenvalues of a real symmetric matrix are real.

注意：假如 $S$ 是复矩阵，需要 $S = \bar{S}^T$ 才能保证特征值为实数。

---

假设有 $Sx = \lambda_1 x$ 和 $Sy = \lambda_2 y$，其中 $\lambda_1 \neq \lambda_2$。

对于 $Sy = \lambda_2 y$，左乘 $x^T$，得到 $x^T S y = \lambda_2 x^T y$。

又因为 $S = S^T$，所以 $x^T S y = (S x)^T y = (\lambda_1 x)^T y = \lambda_1 x^T y$。

所以可得 $\lambda_1 x^T y = \lambda_2 x^T y$。

所以 $(\lambda_1 - \lambda_2) x^T y = 0$。

所以 $x^T y = 0$。

Orthogonal Eigenvectors Eigenvectors of a real symmetric matrix (when they correspond to different eigenvalues) are always perpendicular.

注意：不是所有特征向量都正交，对应不同特征值的特征向量一定正交，同一特征值的特征向量有可能正交。对称矩阵中，同一特征值的特征向量可以通过施密特正交化变成正交的。

求一个实对称矩阵的特征值和特征向量和 $Q$ 的步骤：

1. 求解特征多项式 $det(S - \lambda I) = 0$，得到所有特征值 $\lambda_1, \lambda_2, \ldots, \lambda_n$。

2. 对于每个特征值 $\lambda_i$，求解齐次线性方程组 $(S - \lambda_i I)x = 0$，得到对应的特征向量 $x_i$。

3. 此时特征向量是正交的但未归一化，将每个特征向量 $x_i$ 归一化，得到单位特征向量 $q_i = \frac{x_i}{||x_i||}$。

4. 将所有特征向量组成矩阵 $Q = [q_1, q_2, \ldots, q_n]$，并将对应的特征值组成对角矩阵 $\Lambda = diag(\lambda_1, \lambda_2, \ldots, \lambda_n)$。

比如

$$S = \begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix}$$

1. 求解特征多项式，得到特征值 $\lambda_1 = 0$ 和 $\lambda_2 = 5$。

   $$det \begin{bmatrix} 1 - \lambda & 2 \\ 2 & 4 - \lambda \end{bmatrix} = (1 - \lambda)(4 - \lambda) - 4 = \lambda^2 - 5\lambda = \lambda(\lambda - 5) = 0$$

2. 对于 $\lambda_1 = 0$，求解 $(S - 0I)x = 0$：

   $$\begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = 0$$

   解得特征向量 $x_1 = \begin{bmatrix} 2 \\ -1 \end{bmatrix}$。

   对于 $\lambda_2 = 5$，求解 $(S - 5I)x = 0$：

   $$\begin{bmatrix} -4 & 2 \\ 2 & -1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = 0$$

   解得特征向量 $x_2 = \begin{bmatrix} 1 \\ 2 \end{bmatrix}$。

3. 归一化特征向量：

   $$q_1 = \frac{1}{\sqrt{5}} \begin{bmatrix} 2 \\ -1 \end{bmatrix}, q_2 = \frac{1}{\sqrt{5}} \begin{bmatrix} 1 \\ 2 \end{bmatrix}$$

4. 组成矩阵 $Q$ 和 $\Lambda$：

   $$Q = \frac{1}{\sqrt{5}} \begin{bmatrix} 2 & 1 \\ -1 & 2 \end{bmatrix}, \Lambda = \begin{bmatrix} 0 & 0 \\ 0 & 5 \end{bmatrix}$$

$$S = Q \Lambda Q^T = \frac{1}{\sqrt{5}} \begin{bmatrix} 2 & 1 \\ -1 & 2 \end{bmatrix} \begin{bmatrix} 0 & 0 \\ 0 & 5 \end{bmatrix} \frac{1}{\sqrt{5}} \begin{bmatrix} 2 & -1 \\ 1 & 2 \end{bmatrix} = \begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix}$$

对于任意 $A$，$A^T A$ 和 $A A^T$ 都是对称矩阵。

$A = Q \Lambda Q^T$，则 $A^T A = (Q \Lambda Q^T)^T (Q \Lambda Q^T) = Q \Lambda^T Q^T Q \Lambda Q^T = Q \Lambda^2 Q^T$ 以及 $A A^T = (Q \Lambda Q^T)(Q \Lambda Q^T)^T = Q \Lambda Q^T Q \Lambda^T Q^T = Q \Lambda^2 Q^T$。（在 SVD 分解有用）

相似矩阵

若存在 $M$ 和 $M^{-1}$，使得 $B = M^{-1} A M$，则称矩阵 $A$ 和 $B$ 是相似矩阵。

相似矩阵有相同的特征值。

假设有 $A x = \lambda x$ 和 $B = M^{-1} A M$。

则有

$$M^{-1} A ( MM^{-1} ) x = \lambda M^{-1} x \to (M^{-1} A M) ( M^{-1} x ) = \lambda ( M^{-1} x )$$

得

$$B ( M^{-1} x ) = \lambda ( M^{-1} x )$$

因此 $B$ 有相同的特征值 $\lambda$，对应的特征向量为 $M^{-1} x$。

显然因为 $\det(B)$ 为特征值的乘积，所以相似矩阵有相同的行列式，以及特征值的和相同推出相同的迹 $tr(B) = tr(A)$。

---

两个矩阵相似，他们的特征值相同，但是相反，两个矩阵特征值相同，并不一定相似。

比如

$$A = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}, B = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$$

后者是一个对角矩阵、单位矩阵，但是它没法取 $M$ 使得 $B = M^{-1} A M$，虽然他们有相同的特征值 $\lambda = 1$。

对于 $cI$，其中 $c$ 是标量，$I$ 是单位矩阵，它的相似矩阵只有它自己。取可逆矩阵 $M$，则有 $M^{-1} (cI) M = c (M^{-1} I M) = cI$。

---

对于 $A$，可以取无穷个可逆矩阵 $M$，使得 $B = M^{-1} A M$，这些 $A$ 的相似矩阵 $B$ 组成一个相似类，他们有相同的特征值、行列式、迹等性质，互相之间可以通过相似变换转换，同时他们表达了同一个线性变换，只是基不同。（基由 $M$ 决定）

在这些相似类中，有的矩阵可以对角化，有的不能对角化。可对角化的可以都由其对角矩阵相似变换得到，其他的则例如上面的 $A = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}$ 这种形式，他们都可以由对应的 Jordan 标准型相似变换而来。对角矩阵这种相似类里面，更特殊的就是 $cI$ 这种形式。

Jordan 标准型 Jordan Normal Form

对于任意矩阵 $A$，都存在一个可逆矩阵 $M$，使得 $J = M^{-1} A M$，其中 $J$ 是 Jordan 标准型矩阵。

$J$ 是由 Jordan 块组成的块对角矩阵。Jordan 块是一个上三角矩阵，对角线上的元素都是同一个标量 $\lambda$，紧接着主对角线上方的元素（上次对角线）全是 1，其余元素全是 0。

例如，矩阵

$$J = \begin{bmatrix} \lambda & 1 & 0 \\ 0 & \lambda & 0 \\ 0 & 0 & \mu \end{bmatrix}$$

有两个 Jordan 块：一个是 $2 \times 2$ 的块

$$\begin{bmatrix} \lambda & 1 \\ 0 & \lambda \end{bmatrix}$$

，对应特征值 $\lambda$，另一个是 $1 \times 1$ 的块

$$\begin{bmatrix} \mu \end{bmatrix}$$

，对应特征值 $\mu$。

特殊的，对角矩阵就是 Jordan 标准型的特例，每个 Jordan 块为 $\begin{bmatrix} \lambda_i \end{bmatrix}$。

每个 Jordan 块对应一个特征值 $\lambda$，Jordan 块的大小等于该特征值的代数重数，而几何重数始终为 1。

正定矩阵 Positive Definite Matrix

The number of positive eigenvalues of S equals the number of positive pivots.

正特征值的数量和正主元的数量相等。

所有主子矩阵的行列式为正数

$r = 1, 2, \dots , n$

构建

$$A = \begin{bmatrix} A_r & P \\ Q & R \end{bmatrix} , x = \begin{bmatrix} \mathbf{y} \\ \mathbf{0} \end{bmatrix}, y \neq \mathbf{0}$$

则 $x^TAx = \begin{bmatrix} y^T & \mathbf{0} \end{bmatrix} \begin{bmatrix} A_r & P \\ Q & R \end{bmatrix} \begin{bmatrix} y^T \\ \mathbf{0} \end{bmatrix} = y^T A_r y > 0$

通过构建这样一个 $x = \begin{bmatrix} \mathbf{y} \\ \mathbf{0} \end{bmatrix}$，证明 $y$ 为任意向量的时候，$y^T A_r y > 0$，所以每一个主子矩阵都是正定矩阵，特征值都是正数，行列式为特征值的乘积，所以行列式大于零。

所有主元为正数

因为不需要行交换的情况下，通过高斯消元法，$A = LU$ 将矩阵 $A$ 化为上三角矩阵 $U$，主元就是上三角矩阵的对角线元素，$det(A) = det(L)det(U)$，而 $det(L) = 1$，所以行列式等于主元的乘积，又因为 $det(A) > 0$，所以主元的乘积大于零，而每一个主元又是每一个主子矩阵的行列式与前一个主子矩阵行列式的比值，所以每一个主元都大于零。

TODO: 惯性定理

Energy-based Definition

对于 $Sx = \lambda x$，有 $x^T S x = \lambda x^T x$。

当 $S$ 是正定矩阵时，$\lambda > 0$，所以对于任意 $x$，有 $x^T S x > 0$。

比如

$$S = \begin{bmatrix} a & b \\ b & c \end{bmatrix}, x = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}$$

则有

$$x^T S x = \begin{bmatrix} x_1 & x_2 \end{bmatrix} \begin{bmatrix} a & b \\ b & c \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = a x_1^2 + 2b x_1 x_2 + c x_2^2 > 0$$

因此，正定矩阵可以看作是一个能量函数，将向量 $x$ 映射到一个正的标量值。

If $S$ and $T$ are symmetric positive definite, so is $S + T$

如果 $S$ 和 $T$ 是对称正定矩阵，则 $S + T$ 也是对称正定矩阵。

因为

$$x^T (S + T) x = x^T S x + x^T T x > 0 + 0 = 0$$

显然成立

If the columns of $A$ are independent, then $S = A^T A$ is positive definite.

当 $A$ 是满秩矩阵时，$S = A^T A$ 是正定矩阵。

因为

$$x^T S x = x^T A^T A x = (A x)^T (A x) = || A x ||^2$$

当 $A$ 的列线性无关时，$A x \neq 0$，所以 $|| A x ||^2 > 0$。

---

综上，当 $S$ 是正定矩阵，有以下五个等价条件：

1. 所有特征值均为正数。

2. 所有主元均为正数。

3. 对于所有非零向量 $x$，有 $x^T S x > 0$。

4. 存在满秩矩阵 $A$，使得 $S = A^T A$。

5. 所有左上三角子矩阵的行列式均为正数，即

   $$det \begin{bmatrix} s_{11} \end{bmatrix} > 0, det \begin{bmatrix} s_{11} & s_{12} \\ s_{21} & s_{22} \end{bmatrix} > 0, \ldots, det(S) > 0$$

Positive Semidefinite Matrices 正半定矩阵

当矩阵 $S$ 满足对于所有非零向量 $x$，有 $x^T S x \geq 0$ 时，称其为正半定矩阵，这包括正定矩阵和一些奇异矩阵。

以及它的特征值 $\lambda$ 满足 $\lambda_i \geq 0$。

比如

$$S = \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix}$$

和

$$T = \begin{bmatrix} 2 &-1 & -1 \\ -1 & 2 & -1 \\ -1 & -1 & 2 \end{bmatrix}$$

同时，将 $S$ 分解为 $A^TA$，$R(A^TA) = 1$，比如

$$A^T A = \begin{bmatrix} 1 & 1 \\ 2 & 2 \end{bmatrix} \begin{bmatrix} 1 & 2 \\ 1 & 2 \end{bmatrix} = \begin{bmatrix} 2 & 4 \\ 4 & 8 \end{bmatrix}$$

$ax^2 + 2bxy + cy^2 = 1$ 和 二次型

给定二次曲线方程，$f(x, y) = a x^2 + 2b xy + c y^2$，可以将其表示为矩阵形式：

$$x^TSx = \begin{bmatrix} x & y \end{bmatrix} \begin{bmatrix} a & b \\ b & c \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = a x^2 + 2b xy + c y^2$$

当 $S$ 是正定矩阵时，$x^T S x = 1$ 描述的是斜着的椭圆。

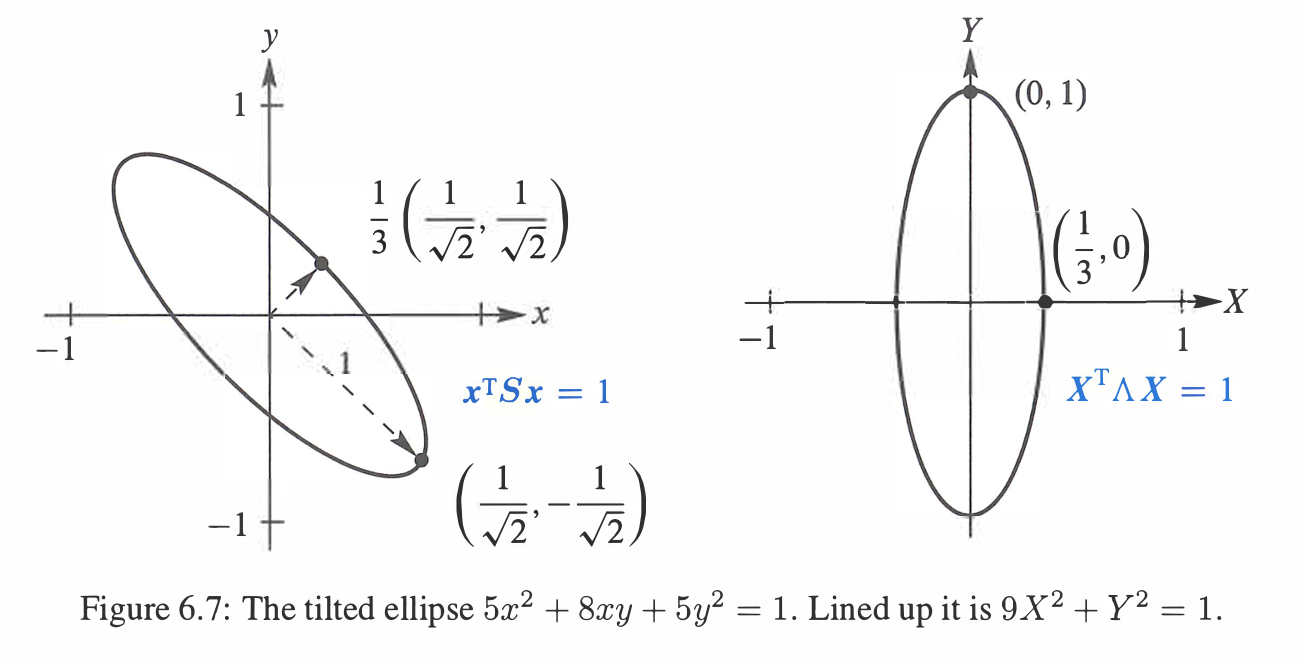
通过配方法，可以将其化为标准形式：

比如

$$5x^2 + 8xy + 5y^2 = 1$$

可以写成矩阵形式：

$$\begin{bmatrix} x & y \end{bmatrix} \begin{bmatrix} 5 & 4 \\ 4 & 5 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = 1$$

根据 $S = Q \Lambda Q^T$，计算出 $Q$ 和 $\Lambda$：

计算矩阵的特征值和特征向量：

$$det \begin{bmatrix} 5 - \lambda & 4 \\ 4 & 5 - \lambda \end{bmatrix} = (5 - \lambda)^2 - 16 = \lambda^2 - 10\lambda + 9 = 0$$

解得特征值为 $\lambda_1 = 9$ 和 $\lambda_2 = 1$。

对应的特征向量为 $x_1 = \begin{bmatrix} 1 \\ 1 \end{bmatrix}$ 和 $x_2 = \begin{bmatrix} 1 \\ -1 \end{bmatrix}$。

将特征向量归一化，得到正交矩阵：

$$Q = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}$$

The axes of the tilted ellipse point along those eigenvectors.

由图可见，椭圆的主轴与特征向量方向一致。

它的主轴长度与特征值相关，主半轴长度为 $\frac{1}{\sqrt{\lambda_1}}$，半短轴长度为 $\frac{1}{\sqrt{\lambda_2}}$。

在这里，主半轴长度为 $\frac{1}{\sqrt{9}} = \frac{1}{3}$，半短轴长度为 $\frac{1}{\sqrt{1}} = 1$。

因为是斜着的，所以两个长短轴各端点分别为

$$\left( \pm \frac{1}{3\sqrt{2}}, \pm \frac{1}{3\sqrt{2}} \right)$$

和

$$\left( \pm \frac{1}{\sqrt{2}}, \mp \frac{1}{\sqrt{2}} \right)$$

---

1. The tilted ellipse is associated with S. Its equation is x T Sx = l. 倾斜椭圆对应的是 矩阵 $S$，其方程为 $x^T S x = 1$。
2. The lined-up ellipse is associated with A. Its equation is XT AX = 1. 对齐椭圆对应的是 矩阵 $A$，其方程为 $X^T \Lambda X = 1$。
3. The rotation matrix that lines up the ellipse is the eigenvector matrix Q. 旋转矩阵 $Q$ 可以将椭圆对齐。

用旋转矩阵 $Q$ 将 椭圆对齐：

将 $x$ 和 $y$ 变换到 $X$ 和 $Y$，$x = Q X$，即

$$\begin{bmatrix} x \\ y \end{bmatrix} = Q \begin{bmatrix} X \\ Y \end{bmatrix}$$

代入原方程 $x^T S x = 1$，得到 $(QX)^T S (QX) = 1$，即

$$\begin{bmatrix} X & Y \end{bmatrix} Q^T S Q \begin{bmatrix} X \\ Y \end{bmatrix} = 1$$

因为 $Q^T S Q = \Lambda$，所以有

$$\begin{bmatrix} X & Y \end{bmatrix} \Lambda \begin{bmatrix} X \\ Y \end{bmatrix} = 1$$

代入

$$\Lambda = \begin{bmatrix} 9 & 0 \\ 0 & 1 \end{bmatrix}$$

得

$$9X^2 + Y^2 = 1$$

就是对齐后的椭圆方程，这两个椭圆只是角度不同。

---

给定二次齐次函数

$$f(x_1, x_2, \ldots, x_n) = a_{11} x_1^2 + a_{22} x_2^2 + \ldots + a_{nn} x_n^2 + 2a_{12} x_1 x_2 + 2a_{13} x_1 x_3 + \ldots + 2a_{n-1,n} x_{n-1} x_n$$

当 $j \geq i$ 时，取 $a_{ij} = a_{ji}$，则拆分得 $2a_{ij}x_i x_j = a_{ij}x_ix_j + a_{ji}x_jx_i$

$$f(x_1, x_2, \ldots, x_n) = a_{11} x_1^2 + a_{12} x_1 x_2 + \ldots + a_{1n} x_1 x_n + a_{21} x_2 x_1 + a_{22} x_2^2 + \ldots + a_{2n} x_2 x_n + \ldots + a_{n1} x_n x_1 + a_{n2} x_n x_2 + \ldots + a_{nn} x_n^2 = \sum_{i=1}^{n} \sum_{j=1}^{n} a_{ij} x_i x_j$$

将其用矩阵表示，

$$f(x) = x_1(a_{11}x_1 + a_{12}x_2 + \ldots + a_{1n}x_n) + x_2(a_{21}x_1 + a_{22}x_2 + \ldots + a_{2n}x_n) + \ldots + x_n(a_{n1}x_1 + a_{n2}x_2 + \ldots + a_{nn}x_n)$$

$$= \begin{pmatrix} x_1 & x_2 & \ldots & x_n \end{pmatrix} \begin{bmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{bmatrix} \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} = x^T A x$$

因此，二次齐次函数可以表示为矩阵形式 $x^T A x$。

规范式指的是 $\lambda_1 y_1^2 + \lambda_2 y_2^2 + \ldots + \lambda_n y_n^2 = 1$，当 $n = 2$时，就是椭圆的标准方程。

利用特征值和特征向量，可以将二次齐次函数化为规范式。

当 $A = Q \Lambda Q^T$ 时，有

$$x^T A x = x^T Q \Lambda Q^T x$$

令 $y = Q^T x$，则有

$$x^T A x = y^T \Lambda y = \lambda_1 y_1^2 + \lambda_2 y_2^2 + \ldots + \lambda_n y_n^2$$

这样可以通过判断特征值的符号，来判断二次齐次函数是否正定、负定还是不定，从而来判断二次齐次函数的截面形状（$x^T A x = 1$）和几何形状：

• 当所有特征值均为正时，表示一个椭圆（或椭球体）。

• 当所有特征值均为负时，表示一个椭圆（或椭球体），但方向相反。

• 当特征值有正有负时，表示一个双曲线（或双曲面）。

和圆锥曲线的圆锥和截面有啥关系吗？

多元函数判断极小值 Test for a Minimum

对于一元函数 $f(x)$，最低点的情况是一阶导为 0，二阶导大于 0。

对于二元函数 $f(x, y)$，当且仅当：

$$\frac{\partial F}{\partial x}(x_0,y_0) = 0, \quad \frac{\partial F}{\partial y}(x_0,y_0) = 0$$

并且 Hessian 矩阵 (S) 正定，即：

$$H = \begin{bmatrix} \frac{\partial^2 F}{\partial x^2} & \frac{\partial^2 F}{\partial x \partial y} \\ \frac{\partial^2 F}{\partial y \partial x} & \frac{\partial^2 F}{\partial y^2} \end{bmatrix}$$

类比一元函数对 $x$ 进行求导，二元函数需要对 $x$ 和 $y$ 分别求偏导数（对某个参数求导时，将其他参数视为常数。

其中，梯度指的是多元函数在各个方向上的一阶偏导数组成的向量：

$$\nabla F = \begin{bmatrix} \frac{\partial F}{\partial x} \\ \frac{\partial F}{\partial y} \end{bmatrix}$$

当梯度为 0 时，函数在该点处有极值。

二次函数的二阶导又需要在一阶导的基础上，继续对 $x$ 和 $y$ 分别求偏导数，得到四种情况：

1. 对 $x$ 求两次偏导数，得到 $\frac{\partial^2 F}{\partial x^2}$。

2. 先对 $x$ 求偏导数，再对 $y$ 求偏导数，得到 $\frac{\partial^2 F}{\partial x \partial y}$。

3. 先对 $y$ 求偏导数，再对 $x$ 求偏导数，得到 $\frac{\partial^2 F}{\partial y \partial x}$。

4. 对 $y$ 求两次偏导数，得到 $\frac{\partial^2 F}{\partial y^2}$。

Hessian 矩阵指的是多元函数在各个方向上的二阶偏导数组成的矩阵。

更高阶的多元函数同理，共同构成 k 阶张量。

当 Hessian 矩阵正定时，说明在任意方向上都“向上弯”，函数在该点处有极小值。

如何判断弯曲程度，可以用泰勒近似：

$$F(x,y) \approx F(x_0,y_0) + \nabla F(x_0,y_0)^T \begin{bmatrix} x - x_0 \\ y - y_0 \end{bmatrix} + \frac{1}{2} \begin{bmatrix} x - x_0 & y - y_0 \end{bmatrix} H \begin{bmatrix} x - x_0 \\ y - y_0 \end{bmatrix}$$

因为在 $(x_0, y_0)$ 处，$F(x_0,y_0) = 0$，梯度为 0，所以取决于

$$\begin{bmatrix} x - x_0 & y - y_0 \end{bmatrix} H \begin{bmatrix} x - x_0 \\ y - y_0 \end{bmatrix}$$

考虑上面的二次齐次函数，可以看出其形式与二次函数类似。

$$v = \begin{bmatrix} x - x_0 \\ y - y_0 \end{bmatrix}, \quad f(v) = v^T H v$$

对于任何非零向量 $v$，如果 $f(v) > 0$，即当 Hessian 矩阵正定，函数在该点处弯曲向上，配合梯度为 0 则有极小值。

可以利用以下条件判断 Hessian 矩阵是否正定：

1. $\det(H) > 0$ 且 $f_{xx} > 0$。

2. 特征值均为正数。

秩-零化度定理

像空间和核空间

对于变换，都是将向量从一个空间映射到另一个空间。

所有输出向量构成的集合为像空间，所有被映射到零向量的输入向量构成的集合叫核空间或零空间。

---

秩-零化度定理：

$$\dim(\ker(A)) + R(A) = \dim(V)$$

几何证明：

1. 取核空间中的一组基为 $\{u_1, u_2, \ldots, u_k\}$，则 $\dim(\ker(A)) = k$。

2. 将基扩展为整个空间 $V$ 的一组基 $\{u_1, u_2, \ldots, u_k, v_{k+1}, v_{k+2}, \ldots, v_n\}$，则 $\dim(V) = k + m = n$。

3. 证明 $\{A v_{k+1}, A v_{k+2}, \ldots, A v_n\}$ 是 $\operatorname{Im}(A)$ 的一组基。

   • 线性无关性：假设存在系数 $c_{k+1}, c_{k+2}, \ldots, c_n$ 使得

     $$c_{k+1} A v_{k+1} + c_{k+2} A v_{k+2} + \ldots + c_n A v_n = 0$$

     则有

     $$A (c_{k+1} v_{k+1} + c_{k+2} v_{k+2} + \ldots + c_n v_n) = 0$$

     这意味着 $w = c_{k+1} v_{k+1} + c_{k+2} v_{k+2} + \ldots + c_n v_n \in \ker(A)$。

     所以 $w$ 可以表示为核空间基的线性组合：

     $$w = d_1 u_1 + d_2 u_2 + \ldots + d_k u_k$$

     因此，$c_{k+1} v_{k+1} + c_{k+2} v_{k+2} + \ldots + c_n v_n - d_1 u_1 - d_2 u_2 - \ldots - d_k u_k = 0$

     因为 $u_1, u_2, \ldots, u_k, v_{k+1}, v_{k+2}, \ldots, v_n$ 线性无关，所以所有系数均为零：

     $$c_{k+1} = c_{k+2} = \ldots = c_n = 0$$

     所以 $A v_{k+1}, A v_{k+2}, \ldots, A v_n$ 线性无关。

     因此，回到假设可知，$\{A v_{k+1}, A v_{k+2}, \ldots, A v_n\}$ 线性无关。

   • 张成性：对于任意 $y \in \operatorname{Im}(A)$，存在 $x \in V$ 使得 $A x = y$。将 $x$ 用基展开：

     $$x = a_1 u_1 + a_2 u_2 + \ldots + a_k u_k + b_{k+1} v_{k+1} + b_{k+2} v_{k+2} + \ldots + b_n v_n$$

     因为 $A u_i = 0$ 对所有 $i = 1, 2, \ldots, k$ 成立，

     则有

     $$A x = A (b_{k+1} v_{k+1} + b_{k+2} v_{k+2} + \ldots + b_n v_n) = b_{k+1} A v_{k+1} + b_{k+2} A v_{k+2} + \ldots + b_{n} A v_n$$

     所以 $y$ 可以表示为 $\{A v_{k+1}, A v_{k+2}, \ldots, A v_n\}$ 的线性组合。

因此，$\{A v_{k+1}, A v_{k+2}, \ldots, A v_n\}$ 张成 $\operatorname{Im}(A)$。

因此，$\dim(\operatorname{Im}(A)) = n - k$。

综上所述，有

$$\dim(\ker(A)) + R(A) = k + (n - k) = n = \dim(V)$$

SVD 分解

对于任意 $A$ 可以分解为 $A = U \Sigma V^T$，其中 $U$ 和 $V$ 是正交矩阵，$\Sigma$ 是对角矩阵，且对角线上的元素非负且按降序排列。

首先考虑试着找到 $A v_i = \sigma_i u_i$，其中 $v_i$ 和 $u_i$ 分别是 $V$ 和 $U$ 的列向量，$\sigma_i$ 是 $\Sigma$ 的对角线元素。这里的几何意义是找到一个在行空间上的单位正交基 $\{v_1, v_2, \ldots, v_n\}$，使得通过 $A$ 映射到列空间上时，得到的向量 $\{u_1, u_2, \ldots, u_m\}$ 也是正交的，并且每个向量的长度被缩放了一个因子 $\sigma_i$。

对于零空间中的向量 $v_j， n \geq j \gt r$，有 $A v_j = 0$，对应的 $\sigma_j = 0$。

为了找到这些向量和缩放因子，可以考虑 $A^T = V \Sigma^T U^T$，得到

$$A^T A = (V \Sigma^T U^T)(U \Sigma V^T) = V \Sigma^T \Sigma V^T = V \Sigma^2 V^T$$

因为 $A^TA$ 是对称矩阵，可以进行特征值分解，所以 $V$ 是 $A^TA$ 的特征向量矩阵，$\Sigma^2$ 是对应的特征值对角矩阵。$V$ 和 $\Sigma$ 可以计算得到。

以及，$A A^T = U \Sigma \Sigma^T U^T = U \Sigma^2 U^T$，所以 $U$ 是 $A A^T$ 的特征向量矩阵，$\Sigma^2$ 也是对应的特征值对角矩阵，也可以计算得到。

从四大子空间上看：

对于 $v_1, v_2, \ldots, v_r$，它们是行空间的基，$A v_i = \sigma_i u_i$ 映射到列空间上

对于 $v_{r+1}, v_{r+2}, \ldots, v_n$，它们是零空间的基，$A v_j = 0$ 映射到零向量，对应的 $\sigma_j = 0$。

对于 $u_1, u_2, \ldots, u_r$，它们是列空间的基

对于 $u_{r+1}, u_{r+2}, \ldots, u_m$，它们是左零空间的基

从几何上看，SVD 分解可以看作是一个线性变换的三个步骤：

1. 先旋转：通过正交矩阵 $V^T$，将输入向量旋转到一个新的坐标系中。

2. 再缩放：通过对角矩阵 $\Sigma$，在新的坐标系中对各个方向进行缩放。

3. 最后旋转：通过正交矩阵 $U$，将缩放后的向量旋转到最终的输出坐标系中。

此外，因为 $A^T A$ 是半正半定矩阵，所以它的特征值非负，因此 $\Sigma$ 的对角线元素 $\sigma_i$ 也是非负的。