Gobang

封面取自 OI Wiki Alpha–Beta 剪枝

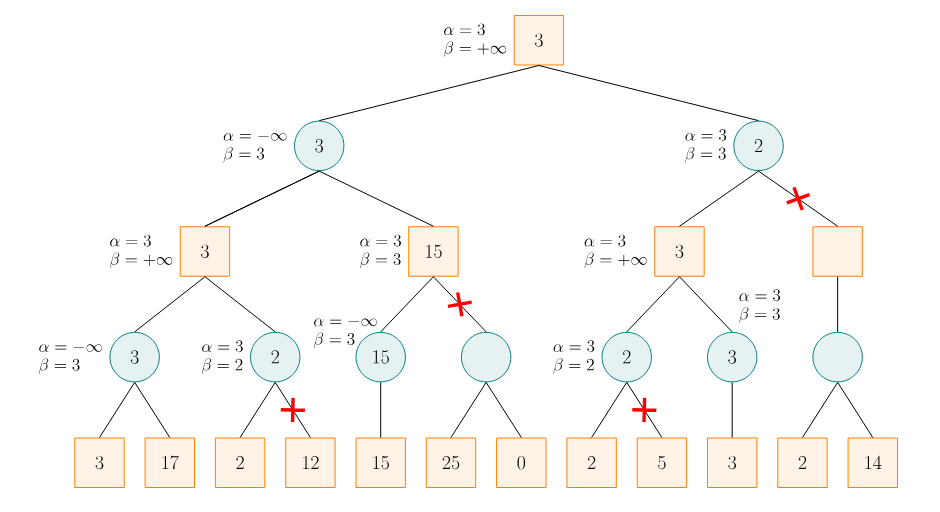
大概花了一下午，C++ 期末作业做了个简单的 AI 五子棋，使用 minimax 算法和 alpha-beta 剪枝。

记录一下如何实现：

1. 需要有评估函数，评估下一步棋的好坏。
   取棋盘上所有的连续的五子组合，除去五个空的情况，然后从黑白两方，分别通过连成了哪些模式，累加双方得分，最后用黑方得分减去白方得分，作为当前棋盘的评估值。

2. 选择落子位置时，只考虑当前棋盘上有棋子的格子周围一定范围内的空格，避免搜索过多无意义的位置。

3. 实现 minimax 算法，递归地模拟双方落子，直到达到设定的搜索深度。
   双方都假定对方会在己方落子后，会选择对己方最不利的落子。因此己方需要选择对方无论如何落子，都会使己方评估值的最小值最大的落子，以保证己方利益能够最大化。

   我要得分最高，对方要让我得分最低，那么对方让我得分低，但比其他低的相对最高的，就是我得分最高的选择

4. 使用 alpha-beta 剪枝，减少不必要的搜索。
   在递归搜索过程中，维护两个值 alpha 和 beta，分别表示当前己方能够获得的最小评估值和对方能够获得的最大评估值。

   己方遍历所有空位，然后对方也根据己方落子，评估剩余空位。如果在评估前 n 个落子时，得出己方最小得到的评估值为 $\alpha$，那么在评估后续己方落子时，对方不断尝试剩余空位，尝试找到最小的下法，使得 $\beta$ 尽可能小。

   如果对方发现可以有某个落子，得到 $\beta < \alpha$ 的评估值，那么对方肯定会选择这个落子而不是其他落子，使得己方获得更低的评估值，己方肯定也不会选择这个己方落子，所以后续该己方落子所对应的对方落子就不需要再继续评估了，达到剪枝的目的。

   我下 A / B，对面接下来可以下 C/D / 和 E/F, 如果下 A 我最低可以拿到 10 -> alpha，而下 B 之后对方下 E 的话我只能拿到 1 -> beta，那么 beta < alpha，对方肯定下 E，既然我知道下 B 对方必下 E，则我也不会下 B 而会下 A，那么没人在乎 F 是多少，反正下 B 必下 E，所以不用计算 F 的评估值。

   反之如果遍历完 E 和 F 以及后续剩下的，都没有让 beta < alpha 的情况，那么说明下 B 比下 A 更好，我就会选择下 B。

评估规则很简单，只是单纯检测了连子，有空再优化吧，应该把五子的视野扩到到六子？

int pattern_score(int pattern[5], int player)
{
    int opponent = (player == 1) ? 2 : 1;

    // Check five in a row
    // Count player and opponent
    int player_count = 0, opponent_count = 0, empty_count = 0;
    bool all_player = true;
    for (int i = 0; i < 5; ++i) {
        if (pattern[i] != player)
            all_player = false;
        
        if (pattern[i] == player)
            player_count++;
        else if (pattern[i] == opponent)
            opponent_count++;
        else
            empty_count++;
    }

    if (all_player)
        return 100000;

    if (opponent_count > 0)
        return 0; // opponent blocks

    switch (player_count)
    {
    case 4: // 01111 or 11110 or 11101
        return (pattern[0] == 0 && pattern[4] == 0) ? 5000 : 500;
    case 3:
        if (pattern[0] == 0 && pattern[4] == 0)
            return 500;
        else if (pattern[0] == 0 || pattern[4] == 0)
            return 100;
        else
            return 0;
    case 2:
        if (pattern[0] == 0 && pattern[4] == 0)
            return 50;
        else
            return 10;
    case 1:
        return 1;
    default:
        return 0;
    }
}

代码见 z0z0r4/gobang

参考：OI Wiki Alpha–Beta 剪枝

这里放一次对局的记录

Gobang Game Initializing!
Enter save file name (or press Enter for default 'gobang_save.dat'):
Checking for existing game state file: gobang_save.dat
No existing game state file found. Starting a new game.
Choose Game Mode:
1. Player vs Player
2. You (Black) vs AI (White)
3. AI (Black) vs You (White)
3

Current Step: 0
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
2 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
3 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
4 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
5 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
6 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
7 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
AI (Black) is thinking...
AI plays at (4, 4)

Current Step: 1
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
2 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
3 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
4 .  .  .  .  B  .  .  .  .  .  .  .  .  .  .
5 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
6 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
7 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
Player White, enter move (x y) or -1 -1 to undo: 5
5

Current Step: 2
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
2 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
3 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
4 .  .  .  .  B  .  .  .  .  .  .  .  .  .  .
5 .  .  .  .  .  W  .  .  .  .  .  .  .  .  .
6 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
7 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
AI (Black) is thinking...
AI plays at (4, 5)

Current Step: 3
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
2 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
3 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
4 .  .  .  .  B  B  .  .  .  .  .  .  .  .  .
5 .  .  .  .  .  W  .  .  .  .  .  .  .  .  .
6 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
7 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
Player White, enter move (x y) or -1 -1 to undo: 4
6

Current Step: 4
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
2 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
3 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
4 .  .  .  .  B  B  W  .  .  .  .  .  .  .  .
5 .  .  .  .  .  W  .  .  .  .  .  .  .  .  .
6 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
7 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
AI (Black) is thinking...
AI plays at (5, 4)

Current Step: 5
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
2 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
3 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
4 .  .  .  .  B  B  W  .  .  .  .  .  .  .  .
5 .  .  .  .  B  W  .  .  .  .  .  .  .  .  .
6 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
7 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
Player White, enter move (x y) or -1 -1 to undo: 3
6

Current Step: 6
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
2 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
3 .  .  .  .  .  .  W  .  .  .  .  .  .  .  .
4 .  .  .  .  B  B  W  .  .  .  .  .  .  .  .
5 .  .  .  .  B  W  .  .  .  .  .  .  .  .  .
6 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
7 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
AI (Black) is thinking...
AI plays at (3, 4)

Current Step: 7
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
2 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
3 .  .  .  .  B  .  W  .  .  .  .  .  .  .  .
4 .  .  .  .  B  B  W  .  .  .  .  .  .  .  .
5 .  .  .  .  B  W  .  .  .  .  .  .  .  .  .
6 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
7 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
Player White, enter move (x y) or -1 -1 to undo: 6
4

Current Step: 8
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
2 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
3 .  .  .  .  B  .  W  .  .  .  .  .  .  .  .
4 .  .  .  .  B  B  W  .  .  .  .  .  .  .  .
5 .  .  .  .  B  W  .  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  .  .  .  .  .  .  .  .
7 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
AI (Black) is thinking...
AI plays at (5, 6)

Current Step: 9
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
2 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
3 .  .  .  .  B  .  W  .  .  .  .  .  .  .  .
4 .  .  .  .  B  B  W  .  .  .  .  .  .  .  .
5 .  .  .  .  B  W  B  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  .  .  .  .  .  .  .  .
7 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
Player White, enter move (x y) or -1 -1 to undo: 6
7

Current Step: 10
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
2 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
3 .  .  .  .  B  .  W  .  .  .  .  .  .  .  .
4 .  .  .  .  B  B  W  .  .  .  .  .  .  .  .
5 .  .  .  .  B  W  B  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  W  .  .  .  .  .  .  .
7 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
AI (Black) is thinking...
AI plays at (7, 3)

Current Step: 11
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
2 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
3 .  .  .  .  B  .  W  .  .  .  .  .  .  .  .
4 .  .  .  .  B  B  W  .  .  .  .  .  .  .  .
5 .  .  .  .  B  W  B  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  W  .  .  .  .  .  .  .
7 .  .  .  B  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
Player White, enter move (x y) or -1 -1 to undo: 3
7

Current Step: 12
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
2 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
3 .  .  .  .  B  .  W  W  .  .  .  .  .  .  .
4 .  .  .  .  B  B  W  .  .  .  .  .  .  .  .
5 .  .  .  .  B  W  B  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  W  .  .  .  .  .  .  .
7 .  .  .  B  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
AI (Black) is thinking...
AI plays at (2, 8)

Current Step: 13
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
2 .  .  .  .  .  .  .  .  B  .  .  .  .  .  .
3 .  .  .  .  B  .  W  W  .  .  .  .  .  .  .
4 .  .  .  .  B  B  W  .  .  .  .  .  .  .  .
5 .  .  .  .  B  W  B  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  W  .  .  .  .  .  .  .
7 .  .  .  B  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
Player White, enter move (x y) or -1 -1 to undo: 4
7

Current Step: 14
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
2 .  .  .  .  .  .  .  .  B  .  .  .  .  .  .
3 .  .  .  .  B  .  W  W  .  .  .  .  .  .  .
4 .  .  .  .  B  B  W  W  .  .  .  .  .  .  .
5 .  .  .  .  B  W  B  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  W  .  .  .  .  .  .  .
7 .  .  .  B  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
AI (Black) is thinking...
AI plays at (1, 4)

Current Step: 15
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 .  .  .  .  B  .  .  .  .  .  .  .  .  .  .
2 .  .  .  .  .  .  .  .  B  .  .  .  .  .  .
3 .  .  .  .  B  .  W  W  .  .  .  .  .  .  .
4 .  .  .  .  B  B  W  W  .  .  .  .  .  .  .
5 .  .  .  .  B  W  B  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  W  .  .  .  .  .  .  .
7 .  .  .  B  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
Player White, enter move (x y) or -1 -1 to undo: 2
4

Current Step: 16
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 .  .  .  .  B  .  .  .  .  .  .  .  .  .  .
2 .  .  .  .  W  .  .  .  B  .  .  .  .  .  .
3 .  .  .  .  B  .  W  W  .  .  .  .  .  .  .
4 .  .  .  .  B  B  W  W  .  .  .  .  .  .  .
5 .  .  .  .  B  W  B  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  W  .  .  .  .  .  .  .
7 .  .  .  B  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
AI (Black) is thinking...
AI plays at (1, 2)

Current Step: 17
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 .  .  B  .  B  .  .  .  .  .  .  .  .  .  .
2 .  .  .  .  W  .  .  .  B  .  .  .  .  .  .
3 .  .  .  .  B  .  W  W  .  .  .  .  .  .  .
4 .  .  .  .  B  B  W  W  .  .  .  .  .  .  .
5 .  .  .  .  B  W  B  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  W  .  .  .  .  .  .  .
7 .  .  .  B  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
Player White, enter move (x y) or -1 -1 to undo: 2
3

Current Step: 18
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 .  .  B  .  B  .  .  .  .  .  .  .  .  .  .
2 .  .  .  W  W  .  .  .  B  .  .  .  .  .  .
3 .  .  .  .  B  .  W  W  .  .  .  .  .  .  .
4 .  .  .  .  B  B  W  W  .  .  .  .  .  .  .
5 .  .  .  .  B  W  B  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  W  .  .  .  .  .  .  .
7 .  .  .  B  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
AI (Black) is thinking...
AI plays at (1, 3)

Current Step: 19
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 .  .  B  B  B  .  .  .  .  .  .  .  .  .  .
2 .  .  .  W  W  .  .  .  B  .  .  .  .  .  .
3 .  .  .  .  B  .  W  W  .  .  .  .  .  .  .
4 .  .  .  .  B  B  W  W  .  .  .  .  .  .  .
5 .  .  .  .  B  W  B  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  W  .  .  .  .  .  .  .
7 .  .  .  B  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
Player White, enter move (x y) or -1 -1 to undo: 1
5

Current Step: 20
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 .  .  B  B  B  W  .  .  .  .  .  .  .  .  .
2 .  .  .  W  W  .  .  .  B  .  .  .  .  .  .
3 .  .  .  .  B  .  W  W  .  .  .  .  .  .  .
4 .  .  .  .  B  B  W  W  .  .  .  .  .  .  .
5 .  .  .  .  B  W  B  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  W  .  .  .  .  .  .  .
7 .  .  .  B  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
AI (Black) is thinking...
AI plays at (1, 0)

Current Step: 21
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 B  .  B  B  B  W  .  .  .  .  .  .  .  .  .
2 .  .  .  W  W  .  .  .  B  .  .  .  .  .  .
3 .  .  .  .  B  .  W  W  .  .  .  .  .  .  .
4 .  .  .  .  B  B  W  W  .  .  .  .  .  .  .
5 .  .  .  .  B  W  B  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  W  .  .  .  .  .  .  .
7 .  .  .  B  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
Player White, enter move (x y) or -1 -1 to undo: 1
1

Current Step: 22
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 B  W  B  B  B  W  .  .  .  .  .  .  .  .  .
2 .  .  .  W  W  .  .  .  B  .  .  .  .  .  .
3 .  .  .  .  B  .  W  W  .  .  .  .  .  .  .
4 .  .  .  .  B  B  W  W  .  .  .  .  .  .  .
5 .  .  .  .  B  W  B  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  W  .  .  .  .  .  .  .
7 .  .  .  B  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
AI (Black) is thinking...
AI plays at (4, 3)

Current Step: 23
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 B  W  B  B  B  W  .  .  .  .  .  .  .  .  .
2 .  .  .  W  W  .  .  .  B  .  .  .  .  .  .
3 .  .  .  .  B  .  W  W  .  .  .  .  .  .  .
4 .  .  .  B  B  B  W  W  .  .  .  .  .  .  .
5 .  .  .  .  B  W  B  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  W  .  .  .  .  .  .  .
7 .  .  .  B  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
Player White, enter move (x y) or -1 -1 to undo: 4
3
Position occupied. Try again.

Current Step: 23
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 B  W  B  B  B  W  .  .  .  .  .  .  .  .  .
2 .  .  .  W  W  .  .  .  B  .  .  .  .  .  .
3 .  .  .  .  B  .  W  W  .  .  .  .  .  .  .
4 .  .  .  B  B  B  W  W  .  .  .  .  .  .  .
5 .  .  .  .  B  W  B  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  W  .  .  .  .  .  .  .
7 .  .  .  B  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
Player White, enter move (x y) or -1 -1 to undo: 4
2

Current Step: 24
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 B  W  B  B  B  W  .  .  .  .  .  .  .  .  .
2 .  .  .  W  W  .  .  .  B  .  .  .  .  .  .
3 .  .  .  .  B  .  W  W  .  .  .  .  .  .  .
4 .  .  W  B  B  B  W  W  .  .  .  .  .  .  .
5 .  .  .  .  B  W  B  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  W  .  .  .  .  .  .  .
7 .  .  .  B  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
AI (Black) is thinking...
AI plays at (3, 2)

Current Step: 25
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 B  W  B  B  B  W  .  .  .  .  .  .  .  .  .
2 .  .  .  W  W  .  .  .  B  .  .  .  .  .  .
3 .  .  B  .  B  .  W  W  .  .  .  .  .  .  .
4 .  .  W  B  B  B  W  W  .  .  .  .  .  .  .
5 .  .  .  .  B  W  B  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  W  .  .  .  .  .  .  .
7 .  .  .  B  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
Player White, enter move (x y) or -1 -1 to undo: 2
1

Current Step: 26
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 B  W  B  B  B  W  .  .  .  .  .  .  .  .  .
2 .  W  .  W  W  .  .  .  B  .  .  .  .  .  .
3 .  .  B  .  B  .  W  W  .  .  .  .  .  .  .
4 .  .  W  B  B  B  W  W  .  .  .  .  .  .  .
5 .  .  .  .  B  W  B  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  W  .  .  .  .  .  .  .
7 .  .  .  B  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
AI (Black) is thinking...
AI plays at (2, 5)

Current Step: 27
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 B  W  B  B  B  W  .  .  .  .  .  .  .  .  .
2 .  W  .  W  W  B  .  .  B  .  .  .  .  .  .
3 .  .  B  .  B  .  W  W  .  .  .  .  .  .  .
4 .  .  W  B  B  B  W  W  .  .  .  .  .  .  .
5 .  .  .  .  B  W  B  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  W  .  .  .  .  .  .  .
7 .  .  .  B  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
Player White, enter move (x y) or -1 -1 to undo: 3
3

Current Step: 28
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 B  W  B  B  B  W  .  .  .  .  .  .  .  .  .
2 .  W  .  W  W  B  .  .  B  .  .  .  .  .  .
3 .  .  B  W  B  .  W  W  .  .  .  .  .  .  .
4 .  .  W  B  B  B  W  W  .  .  .  .  .  .  .
5 .  .  .  .  B  W  B  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  W  .  .  .  .  .  .  .
7 .  .  .  B  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
AI (Black) is thinking...
AI plays at (5, 1)

Current Step: 29
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
1 B  W  B  B  B  W  .  .  .  .  .  .  .  .  .
2 .  W  .  W  W  B  .  .  B  .  .  .  .  .  .
3 .  .  B  W  B  .  W  W  .  .  .  .  .  .  .
4 .  .  W  B  B  B  W  W  .  .  .  .  .  .  .
5 .  B  .  .  B  W  B  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  W  .  .  .  .  .  .  .
7 .  .  .  B  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
Player White, enter move (x y) or -1 -1 to undo: 0
6
    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
0 .  .  .  .  .  .  W  .  .  .  .  .  .  .  .
1 B  W  B  B  B  W  .  .  .  .  .  .  .  .  .
2 .  W  .  W  W  B  .  .  B  .  .  .  .  .  .
3 .  .  B  W  B  .  W  W  .  .  .  .  .  .  .
4 .  .  W  B  B  B  W  W  .  .  .  .  .  .  .
5 .  B  .  .  B  W  B  .  .  .  .  .  .  .  .
6 .  .  .  .  W  .  .  W  .  .  .  .  .  .  .
7 .  .  .  B  .  .  .  .  .  .  .  .  .  .  .
8 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
9 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
10 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
11 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
12 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
13 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
14 .  .  .  .  .  .  .  .  .  .  .  .  .  .  .
Player White wins!

--- Game Record ---
Step 1: Player Black -> (4, 4)
Step 2: Player White -> (5, 5)
Step 3: Player Black -> (4, 5)
Step 4: Player White -> (4, 6)
Step 5: Player Black -> (5, 4)
Step 6: Player White -> (3, 6)
Step 7: Player Black -> (3, 4)
Step 8: Player White -> (6, 4)
Step 9: Player Black -> (5, 6)
Step 10: Player White -> (6, 7)
Step 11: Player Black -> (7, 3)
Step 12: Player White -> (3, 7)
Step 13: Player Black -> (2, 8)
Step 14: Player White -> (4, 7)
Step 15: Player Black -> (1, 4)
Step 16: Player White -> (2, 4)
Step 17: Player Black -> (1, 2)
Step 18: Player White -> (2, 3)
Step 19: Player Black -> (1, 3)
Step 20: Player White -> (1, 5)
Step 21: Player Black -> (1, 0)
Step 22: Player White -> (1, 1)
Step 23: Player Black -> (4, 3)
Step 24: Player White -> (4, 2)
Step 25: Player Black -> (3, 2)
Step 26: Player White -> (2, 1)
Step 27: Player Black -> (2, 5)
Step 28: Player White -> (3, 3)
Step 29: Player Black -> (5, 1)
Step 30: Player White -> (0, 6)