learning-notesCSCSAPP

关于 CSAPP - Lecture 04 Floating Point 的浮点数（float）的笔记。

定义

IEEE 754 浮点数标准定义了浮点数的表示方法。

有分为单精度（32 位）和双精度（64 位）。

图片摘自 https://www.wdxtub.com/blog/csapp/thin-csapp-1#ieee-浮点数标准

浮点数分规范化数（normalized numbers）、非规范化数（denormalized numbers）和特殊值三种情况。

对于规范化数，浮点数的表示为：

(−1)s×(1+frac)×2exp−bias(-1)^s \times (1 + frac) \times 2^{exp - bias}

其中：

  • s：符号位，0 表示正数，1 表示负数
  • exp：编码后的指数值
  • bias：指数值的偏移量，2k−1−12^{k-1} - 1。对于单精度浮点数为 127（27−1 2^7 - 1），对于双精度浮点数，bias 为 1023（210−1 2^{10} - 1）
  • frac：尾数部分，表示小数部分

对于非规范化数，浮点数的表示为：

(−1)s×(0+frac)×21−bias(-1)^s \times (0 + frac) \times 2^{1 - bias}

特殊值包括：

  • 正零和负零
    • 正零为所有位均为 0
    • 负零为 s 为 1，其它位均为 0
  • 正无穷和负无穷：exp 全为 1，frac 全为 0
    • 正无穷为 s 为 0，
    • 负无穷为 s 为 1
  • NaN（Not a Number）：exp 全为 1，frac 不全为 0

观察到，浮点数可以省略 frac 的前导 1，这样可以节省存储空间。

但是这样的话无法表示 0，因为如果省略了前导 1，那么 frac 全为 0 时表示的数值为 1.0×2exp−bias 1.0 × 2^{exp - bias} ，永远不可能表示 0，所以需要规定当 exp=0 exp = 0 时，非规范数的式子是 (0+frac)(0 + frac)，这样就可以表示 0 了。

同时，当 exp=0 exp = 0 时，frac 全为 0 时为最大的非规范化数，发现对应的数值为 0.111⋯×20−bias 0.111\dots × 2^{0 - bias} ，与最小的规范化数 exp=1exp = 1 时 1.0×21−bias 1.0 × 2^{1 - bias} 之间的间隔过大，形成断层。

当 exp 为四位，frac为三位，举例说明：

最小的规范化数：
1.0002×2−6=1×164=164=0.0156251.000_2 \times 2^{-6} = 1 \times \frac{1}{64} = \frac{1}{64} = 0.015625

最大的非规范化数：

如果用的是 1−bias 1 - bias ，即：

  • 值 = 0.1112×2−6=(12+14+18)×164=78×164=7512=0.0136718750.111_2 \times 2^{-6} = \left(\frac{1}{2} + \frac{1}{4} + \frac{1}{8}\right) \times \frac{1}{64} = \frac{7}{8} \times \frac{1}{64} = \frac{7}{512} = 0.013671875
  • 差值 = 0.015625−0.013671875=0.0019531250.015625 - 0.013671875 = 0.001953125
  • 百分比为 0.0019531250.015625=12.5% \frac{0.001953125}{0.015625} = 12.5\%

如果用的是 0−bias 0 - bias ，即：

  • 值 = 0.1112×2−7=78×1128=71024=0.00683593750.111_2 \times 2^{-7} = \frac{7}{8} \times \frac{1}{128} = \frac{7}{1024} = 0.0068359375
  • 最小规范数仍为 0.0156250.015625
  • 差值 = 0.015625−0.0068359375=0.00878906250.015625 - 0.0068359375 = 0.0087890625
  • 百分比为 0.00878906250.015625=56.25% \frac{0.0087890625}{0.015625} = 56.25\% ，差距过大。

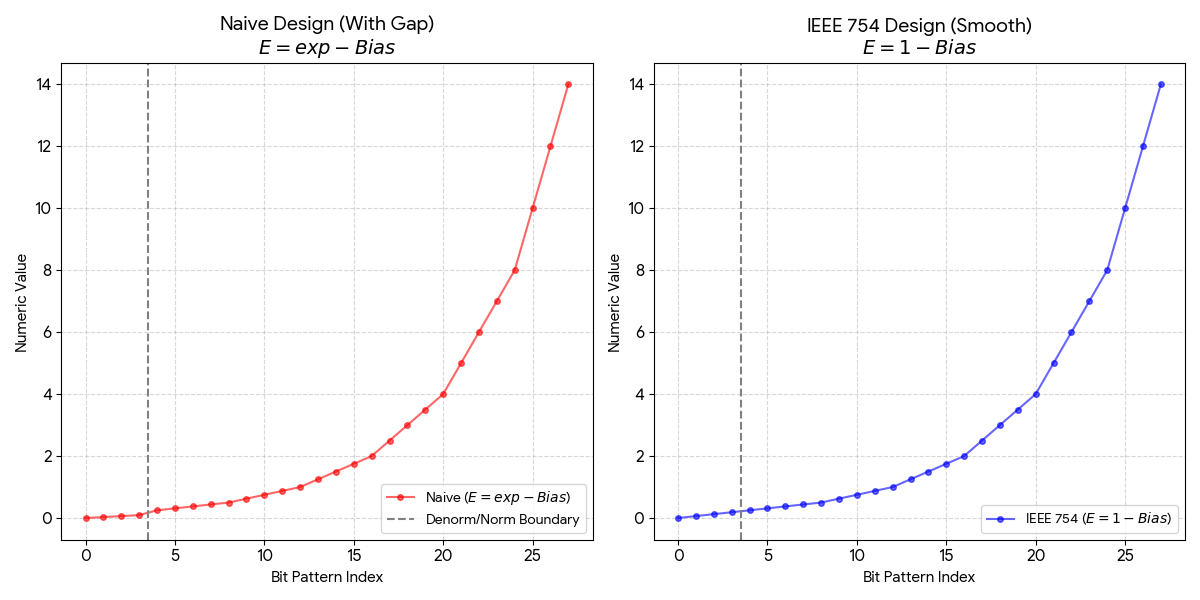
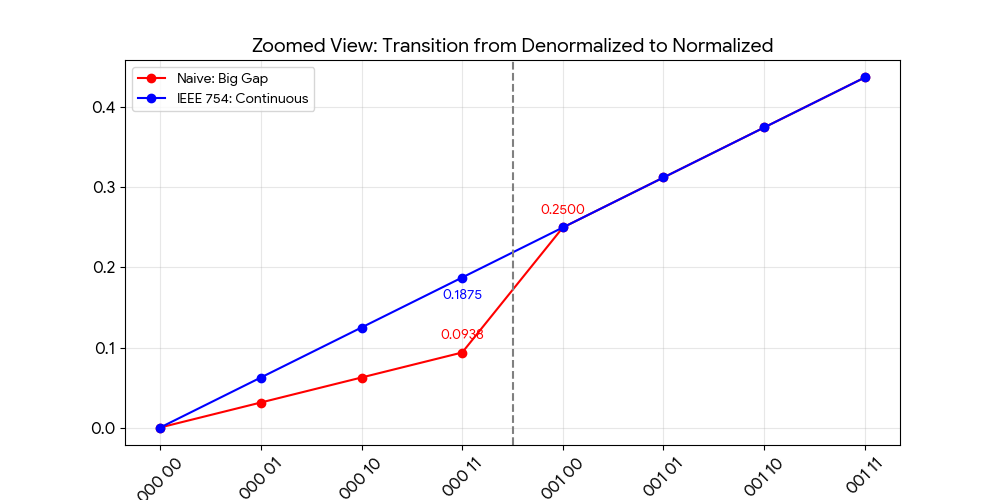
图片生成自 Gemini

图片生成自 Gemini

在非规范化的情况，相邻浮点数间距是一致的。在规范化的情况下，随着 exp 的变化，浮点数间距也会变化。

舍入

浮点数在运算中可能会出现无法精确表示的情况，这时需要进行舍入。

IEEE 754 标准定义了四种舍入方式：

  1. 向最近偶数舍入（Round to Nearest, Even）：将结果舍入到最接近的浮点数，如果结果正好在两个浮点数之间，则舍入到偶数。
  2. 向零舍入（Round toward Zero）：将结果向零方向舍入。
  3. 向正无穷舍入（Round toward +∞）：将结果向正无穷方向舍入。
  4. 向负无穷舍入（Round toward -∞）：将结果向负无穷方向舍入。

默认情况下，IEEE 754 标准采用向最近偶数舍入方式。

实际运算的舍入中，需要考虑尾数后的额外三位 GRS（guard bit, round bit, sticky bit）：

  • G（Guard Bit）：紧接在尾数后的第一位，用于判断舍入方向。
  • R（Round Bit）：紧接在 G 位后的第二位，也用于判断舍入方向。
  • S（Sticky Bit）：尾数后所有位的逻辑或结果，如果尾数后还有非零位，则 S 位为 1，否则为 0。

向最近偶数舍入以 GSR 为 100 为分界线，有三种情况：

  1. 如果 G 位为 0，则直接舍弃 GRS 位，保持尾数不变。对应 GSR 为 000、001、010、011 四种情况，小于 100。
  2. 如果 G 位为 1，且 R 位或 S 位至少有一位为 1，则将尾数加 1。对应 GSR 为 101、110、111 三种情况，大于 100。
  3. 如果 G 位为 1，且 R 位和 S 位均为 0，则检查尾数的最后一位：
    • 如果尾数的最后一位为 0，则直接舍弃 GRS 位，保持尾数不变。
    • 如果尾数的最后一位为 1，则将尾数加 1。对应 GSR 为 100 情况。

三位足以以判断舍入方式，先考虑两位和一位的情况下为什么不能够判断舍入方式：

  1. 只有一位 G 位：

    • 如果 G 位为 0，则可以确定舍弃 G 位，保持尾数不变。
    • 如果 G 位为 1，则无法确定是向偶数舍入还是向上舍入，因为可能是 100 或者 101 或者更大的情况。

  2. 只有两位 G 和 R 位：

    • 如果 G 位为 0，则可以确定舍弃 GR 位，保持尾数不变。
    • 如果 G 位为 1 且 R 位为 1，则可以确定向上舍入。
    • 如果 G 位为 1 且 R 位为 0，则无法确定是向偶数舍入还是向上舍入，因为可能是 100 或者 101 或者更大且 R 位为 0 的情况。（即无法考虑 S 位及其后面的位）

在 G 位为 1 且 R 位为 0 的情况下，加入 S 位后，可以区分出 GRS 为 100（需要考虑尾数最后一位）和 GRS 为 101、110、111（需要向上舍入）的情况，则覆盖了所有情况，第四位没有必要。

浮点数加法

对于浮点数加法，需要对齐指数，然后进行尾数相加，最后进行规范化和舍入。

假设有两个浮点数 F1F_1 和 F2F_2，其中 F1F_1 的指数大于 F2F_2

  1. 对齐指数：将 F2F_2 的尾数右移 exp1−exp2exp_1 - exp_2 位，使得两个浮点数的指数相同。

  2. 尾数相加：根据符号位，进行尾数的加法或减法运算。

  3. 规范化：如果尾数的最高位为 2，则需要将尾数右移一位，并将指数加 1。如果尾数的最高位为 0，则需要将尾数左移，直到最高位为 1，并相应地减少指数。在此过程中，如果指数溢出，则结果为无穷大；如果指数下溢，则结果为零或非规范化数。

  4. 舍入：根据舍入规则，对结果进行舍入。

例子：

假设 F1=1.101×23F_1 = 1.101 \times 2^3，F2=1.011×21F_2 = 1.011 \times 2^1。

  1. 对齐指数：将 F2F_2 的尾数右移 2 位，得到 F2′=0.01011×23F_2' = 0.01011 \times 2^3。

  2. 尾数相加：1.101+0.01011=10.000111.101 + 0.01011 = 10.00011。

  3. 规范化：将尾数右移一位，得到 1.000011×241.000011 \times 2^4。

  4. 舍入：根据舍入规则，对结果进行舍入，比如如果存入三位尾数，结果为 1.000×241.000 \times 2^4，如果存入四位尾数，结果为 1.0001×241.0001 \times 2^4。

浮点数加法不符合结合律，因为在对齐指数时可能会丢失精度。

浮点数乘法

假设有两个浮点数 F1=(−1)s1×M1×2E1F_1 = (-1)^{s_1} \times M_1 \times 2^{E_1} 和 F2=(−1)s2×M2×2E2F_2 = (-1)^{s_2} \times M_2 \times 2^{E_2}。

  1. 符号位相乘：结果的符号位为 s=s1⊕s2s = s_1 \oplus s_2。

  2. 尾数相乘：结果的尾数为 M=M1×M2M = M_1 \times M_2。

  3. 指数相加：结果的指数为 E=E1+E2E = E_1 + E_2

  4. 规范化：如果尾数的最高位为 2，则需要将尾数右移一位，并将指数加 1。在此过程中，如果指数溢出，则结果为无穷大。

  5. 舍入：根据舍入规则，对结果进行舍入。

同样，浮点数乘法不符合结合律，因为在尾数相乘时可能会丢失精度。

类型转换

浮点数与整数之间的转换需要考虑范围和精度的问题。

将 int 转换为 float

int 有 31 位有效位（符号位不算），float 有 23 位尾数，会丢弃掉低位数字，保留高位数字。

将 float/double 转换为 int

截断小数部分，保留整数部分。

如果 float/double 的值超出 int 的表示范围或者是 NaN，则结果未定义，通常会返回 INT_MIN。

将 int/float 转换为 double

int 转换为 double 不会丢失精度，因为 double 有 52 位尾数，足够表示 int 的所有有效位。

float 转换为 double 也不会丢失精度，因为 double 的尾数比 float 多，可以精确表示 float 的值。

Data representation 这几节课里面总是强调这些并非数学意义上的 number，而是一些二进制串，依赖具体定义的 representation 才能被解释为某个数值。