CSAPP Data Alignment

关于对齐的记录。

一开始我起的是 Memory Alignment，但是后面一想其实还有很多地方会用到对齐这个概念，于是改标题为 Data Alignment

定义

当内存地址 $a$ 是 $n$ 的倍数，其中 $n$ 是 2 的幂时，称地址 $a$ 是 $n$ 字节对齐的。

当被访问的数据长度是 $n$ 字节且起始地址 $n$ 字节对齐，那么该数据是对齐的，否则是不对齐的。

基本类型的对齐

• char 是 1 字节对齐

• short 是 2 字节对齐

• int 是 4 字节对齐

• long 是 4 字节对齐（32 位系统）或 8 字节对齐（64 位系统）

• long long 是 4 字节对齐（32 位系统）或 8 字节对齐（64 位系统）

• float 是 4 字节对齐

• double 是 8 字节对齐

• long double 是 8 字节对齐（Visual C++）或者 16 字节对齐（GCC）

• pointer 是 4 字节对齐（32 位系统）或 8 字节对齐（64 位系统）

结构体的对齐

结构体 struct 的根据成员的对齐要求进行对齐，保证每一个成员的起始地址都是对齐的。

首先规则是如下：

• 成员对齐规则： $O_j \equiv 0 \pmod{A_j}$
  （偏移量必须是成员自身对齐要求的倍数）。

• 首地址对齐规则： $P \equiv 0 \pmod{A_{max}}$（结构体起始地址必须是结构体最大对齐要求的倍数）。

• 总大小对齐规则： $Size \equiv 0 \pmod{A_{max}}$（结构体总大小必须是最大对齐要求的倍数）。

其中第二点由编译器的其他细节保证，其他两点需要编译器通过填充（Padding）来实现。

比如下面的结构体，摘自 Wikipedia Data_structure_alignment #Typical_alignment_of_C_structs_on_x86：

struct MixedData
{
    char Data1;
    short Data2;
    int Data3;
    char Data4;
};

• Data1：char，占用 1 字节，起始地址 0，char 对齐要求 1 字节

• 填充 1 字节，使 Data2 起始地址为 2，short 对齐要求 2 字节

• Data2：short，占用 2 字节，起始地址 2

• Data3：int，占用 4 字节，起始地址 4，int 对齐要求 4 字节

• Data4：char，占用 1 字节，起始地址 8，char 对齐要求 1 字节

最后，结构体成员的最大对齐要求是 4 字节，因此结构体的总大小需要是 4 的倍数。当前大小为 9 字节，需要在末尾填充 3 字节，使得总大小为 12 字节。

很显然可以通过调整成员顺序减少填充，减少内存占用：

struct MixedDataReordered
{
    char Data1;
    char Data4;
    short Data2;
    int Data3;
};

最后占用 8 字节，没有填充。

对齐的意义

我这这块比较一头雾水，搜索信息然后试着理解的，如果有谬误请指教

对于早期 RISC 架构下的旧 ARM, MIPS 等的 CPU 非常严格，完全不允许读取不对齐的内存。

实际上 CPU 忽略后三位地址，只能读取字对齐的整段内存地址。

x86 架构的 CPU 则比较宽松，允许读取不对齐的内存，但是会带来性能损失。（通过读取两段内容然后由对齐器重新组合、移位加工来实现）

此外，CPU Cache 也是这样的，它按字读取，如果数据跨行，那就得读取两次。

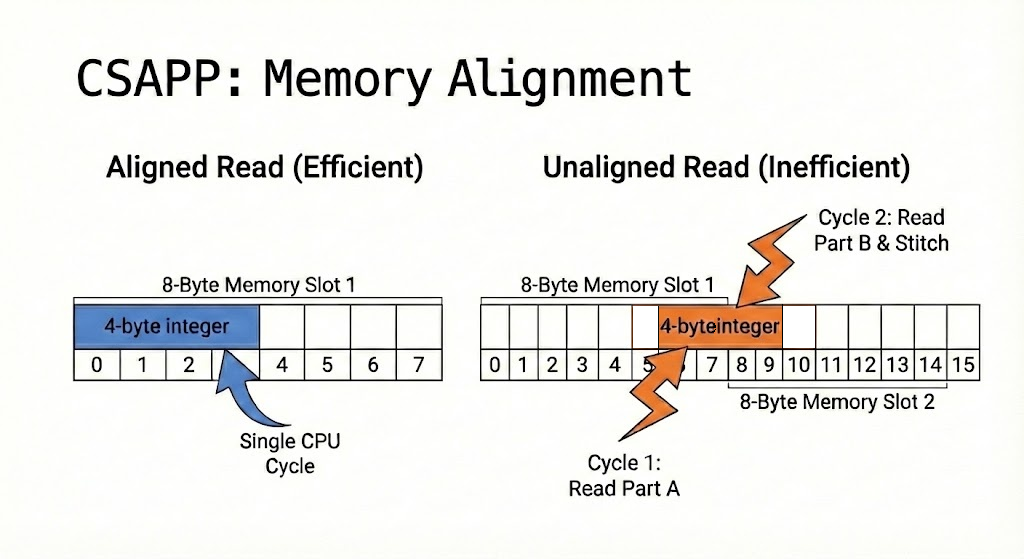
如何对齐

那么为了尽量减少读取次数，就需要将数据对齐。

首先考虑数据的首地址必须对齐，否则后续的元素/成员都无法对齐。

为了达到这点，C 语言标准规定 malloc、alloca、calloc 和 realloc 返回的内存地址至少是 max_align_t 类型对齐的。

以及大多数函数的栈帧必须按 16 字节边界对齐。

考虑由基本类型的数组，它的首地址对齐，数组的每个元素紧挨着，没有 Padding，由于基本类型的长度都是 2 的幂，那么数组的每个元素也都是对齐的。

考虑结构体，它的首地址对齐，如果成员间按需添加 Padding，就能避免一些成员跨越对齐边界。同时添加适当的 Padding 在末尾，能够使得结构体数组的每个元素也都是对齐的。

关于为什么这三条规则就能保证对齐（以下由 AI 生成…）：

假设我们有一个结构体 S，它在内存中的排布遵循以下变量定义：

• $A_j$：结构体中第 $j$ 个成员的对齐要求（如 int 是 4）。

• $O_j$：第 $j$ 个成员相对于结构体首地址的偏移量（Offset）。

• $A_{max}$：整个结构体的对齐要求，定义为 $A_{max} = \max(A_1, A_2, \dots, A_n)$。

• $Size$：结构体的总大小（包含填充字节）。$P$：结构体数组的首地址。

• $Addr(i, j)$：数组中第 $i$ 个元素的第 $j$ 个成员的实际物理地址。

编译器强制执行的三个规则：

• 成员对齐规则： $O_j \equiv 0 \pmod{A_j}$（偏移量必须是成员自身对齐要求的倍数）。

• 首地址对齐规则： $P \equiv 0 \pmod{A_{max}}$（数组起始地址必须是结构体最大对齐要求的倍数）。

• 总大小对齐规则： $Size \equiv 0 \pmod{A_{max}}$（总大小必须是最大对齐要求的倍数）。

要证明的目标是：对于数组中任意元素 $i$ 的任意成员 $j$，其物理地址 $Addr(i, j)$ 都能满足其自身的对齐要求 $A_j$。

即证明：

$$Addr(i, j) \equiv 0 \pmod{A_j}$$

1. 展开物理地址公式根据内存布局，第 $i$ 个元素的第 $j$ 个成员的地址为：

   $$Addr(i, j) = P + (i \times Size) + O_j$$

2. 利用模运算性质拆解我们要计算 $Addr(i, j) \pmod{A_j}$：

   $$Addr(i, j) \pmod{A_j} = (P + i \times Size + O_j) \pmod{A_j}$$

   根据模算术性质，可以拆分为：

   $$(P \pmod{A_j} + (i \times Size) \pmod{A_j} + O_j \pmod{A_j}) \pmod{A_j}$$

3. 证明每一项都为 0 证明 $P \pmod{A_j} = 0$：

   已知规则 2 规定 $P$ 是 $A_{max}$ 的倍数。

   在计算机架构中，对齐要求 $A$ 永远是 2 的幂（1, 2, 4, 8, 16…）。

   因为 $A_{max} = \max(\dots, A_j, \dots)$，所以 $A_{max}$ 必然能被 $A_j$ 整除。

   既然 $P$ 是 $A_{max}$ 的倍数，那么 $P$ 也一定是 $A_j$ 的倍数。

   故：$P \equiv 0 \pmod{A_j}$。

4. 证明 $(i \times Size) \pmod{A_j} = 0$：

   已知规则 3 规定 $Size$ 是 $A_{max}$ 的倍数。

   同理，既然 $Size$ 是 $A_{max}$ 的倍数，它也必然是 $A_j$ 的倍数。无论 $i$ 是多少，$i \times Size$ 依然是 $A_j$ 的倍数。故：$(i \times Size) \equiv 0 \pmod{A_j}$。

5. 证明 $O_j \pmod{A_j} = 0$：

   这直接由规则 1（成员对齐规则）保证。

   故：$O_j \equiv 0 \pmod{A_j}$。

6. 结论将上述三项代入：

   $$Addr(i, j) \pmod{A_j} = (0 + 0 + 0) \pmod{A_j} = 0$$

   证明完毕。

Packing

有时为了节省内存空间，我们希望取消对齐要求，这时可以使用 #pragma pack 指令。

#pragma pack(push, 1) // 保存当前对齐状态，并设置新对齐为 1 字节
struct PackedStruct {
    char a;
    int b;
    char c;
};
#pragma pack(pop)      // 恢复之前的对齐状态

成员变量	类型	大小	偏移量	内存区间
a	char	1 字节	0	[0]
b	int	4 字节	1	[1, 2, 3, 4]
c	char	1 字节	5	[5]

这样一个结构体占用的空间就是 6 字节，没有任何填充。

attribute packed

GCC 也支持通过 __attribute__((packed)) 来实现类似的效果：

struct __attribute__((packed)) PackedStruct {
    char a;
    int b;
    char c;
};

这样定义的结构体同样不会有填充字节，占用最小空间。